MCMC Methods
Metropolis Hastings and other MCMC algorithms are ideal for sampling from multi-dimensional distributions. It is, however, computationally intensive, an unfavourable aspect in addition to the trial and error required (for example, to find an optimal transition kernel). Furthermore, it is difficult to balance the Markov chains mixing and convergence to the posterior.
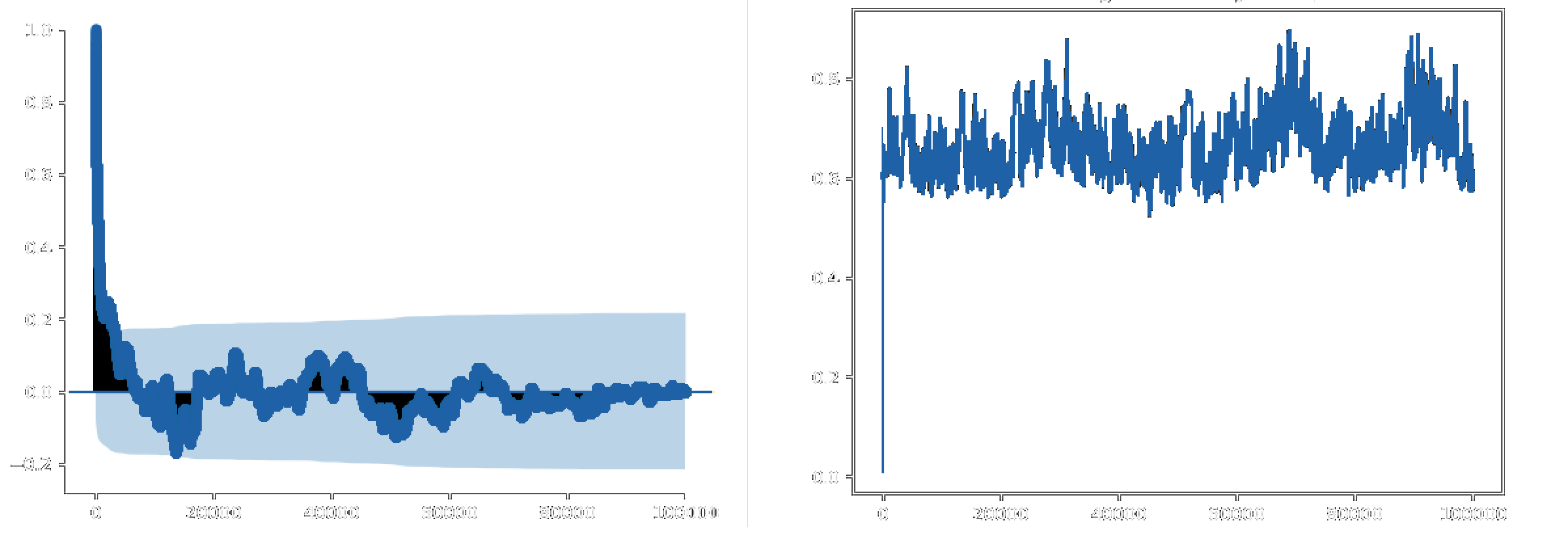
The MH algorithm produces a Markov chain. In order to determine if the algorithm has correctly inferred the posterior, we can inspect trace plots, and autocorrelation functions (ACF). The trace plot, or time series, shows the accepted sample values of the parameter over time (over all iterations). The autocorrelation function indicates how independent different samples from the posterior distribution are – lower autocorrelation indicating more independent results. High autocorrelation indicates that samples drawn don't accurately represent the posterior distribution, and consequently don't provide meaningful information for the solution to the problem. When inspecting the trace plots, three types of mixing behaviour can be observed: the chain can be well mixed, too hot, or too cold:
- If the chain is too cold, the samples from the posterior are correlated, and therefore the overall shape of the posterior fails to be captured. The trace plot appears continuous, and the autocorrelation function does not fall to zero.
- The Markov chain is described as too hot when the transition kernel is too large, causing bad proposals and a low acceptance rate. The trace plot shows that samples spend extended amounts of time in the same position – this is referred to as a “Manhattan skyline”.
- The chain is well mixed when samples are independent and identically distributed when plotted on the posterior. The transition kernel is appropriate in this case, and the trace plot is described as a “fat, hairy caterpillar”.
Examples of the three types of mixing behaviour are shown in Figure 18.
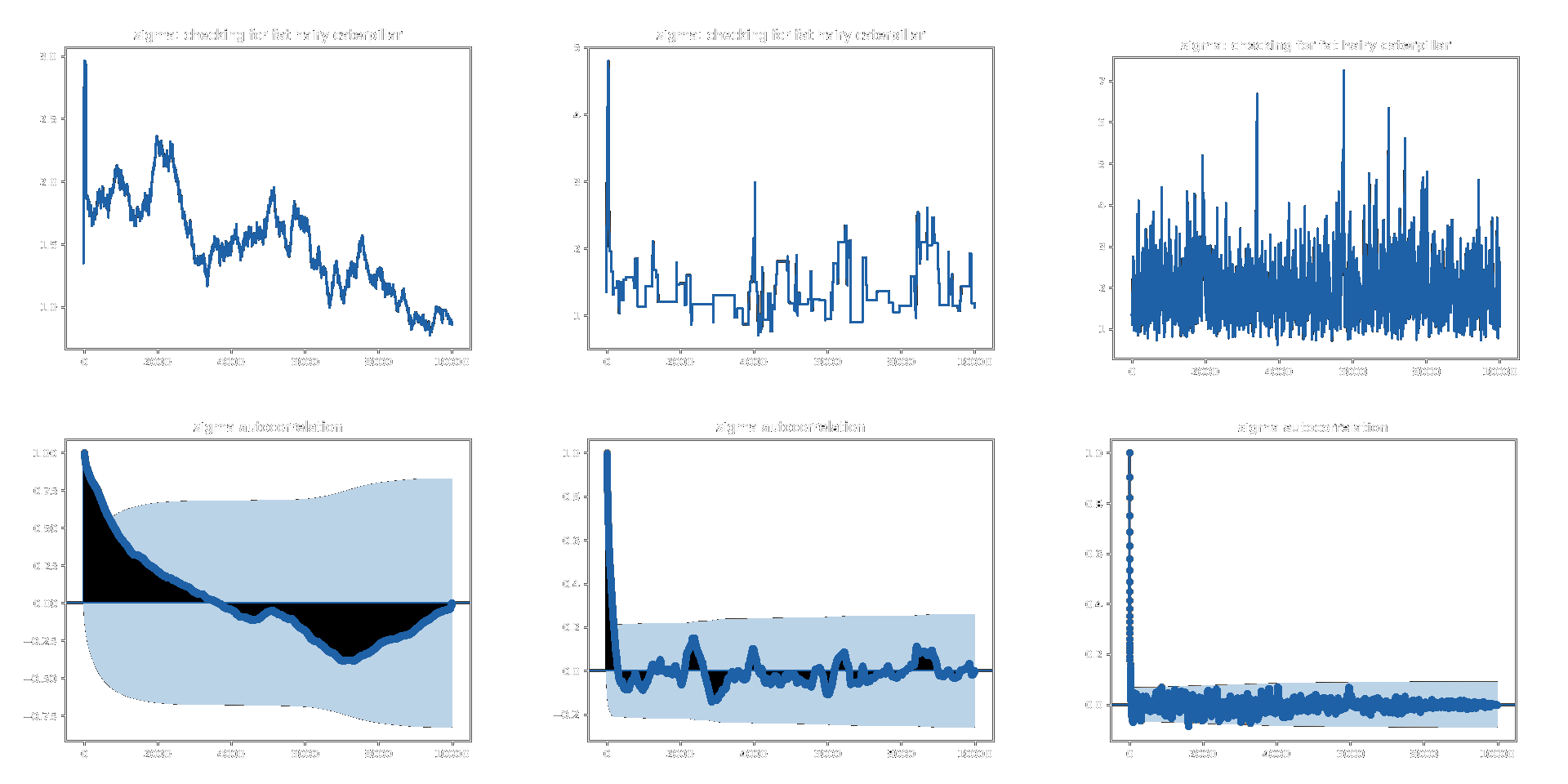
Figure 18: Examples of different types of behaviour that Markov chains can exhibit. From left to right: trace plot and ACF for chains that are cold, hot, and well mixed.
It is often the case that improvements to the posterior inferred can be obtained by increasing the execution time (or the number of iterations of the MCMC method performed). Extensive computational improvements were made to algorithms throughout this project, including the use of tools such as Cython - a superset of the Python programming language, designed to give C-like performance with code that is written mostly in Python. Despite this, running times throughout the course of this project were exceptionally long. More time is required to experiment with the number of iterations performed and total execution time, in order to establish if this significantly improves results.
Future Work and Outlook
Figure 19: This picture is adapted from work by Dicu, 2017.
An additional further development would be to incorporate data from multiple wells measured in the single cell experiment. Each separate well would possess a different value for $X_0$, however we can adopt the assumption that $r$ and $\sigma$ are shared between the different wells within the same experiment. Using data from multiple fluorescence curves should theoretically result in more accurate inference of $r$ (and potentially $\sigma$).
The analysis and investigation carried out in this project has the potential for application to other forms of data, in particular ddPCR (droplet digital PCR). MCMC methods have been implemented on ddPCR data with promise (Wilson and Ellison, 2016), and further investigation of this has not yet been explored extensively. The research and analysis carried out in this project has provided in-depth conceptual understanding of Bayesian inference and MCMC methods, in particular the Metropolis Hastings algorithm. Performing this form of analysis is applicable to a wide range of different types of datasets. Programming frameworks such as PyMC3 and Stan provide tools to perform the types of analysis and inference discussed in this project, in addition to many other analysis methods.